Einteilung nach Topologie
Die Topologie beschreibt die Art wie verschiedene Rechner räumlich miteinander verbunden sind.
Zuerst behandeln wir verschiedene Topologien für P2P-Verbindungen.
Topologien für P2P-Netze
Sterne
|
Jeder Client ist dabei direkt mit dem zentralen Server verbunden, der nicht nur seine normalen Serverdienste anbietet, sondern auch für die gesamte Kommunikation zwischen den Rechnern verantwortlich ist. Will ein Client-Rechner also an einen anderen eine Nachricht schicken, so läuft diese immer über den zentralen Hostrechner. Eine Variante des Sterns findet sich auch bei Broadcast-Netzen in Form der Sternverteiler in 10BASET-Netzen. |
Ringe
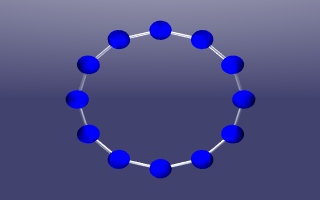 Die ringförmige
Verkabelung zeichnet sich durch einfache Erweiterbarkeit aus, und
ihr größter Nachteil liegt in ihrer Anfälligkeit. Die ringförmige
Verkabelung zeichnet sich durch einfache Erweiterbarkeit aus, und
ihr größter Nachteil liegt in ihrer Anfälligkeit.
Wird der Ring an einer Stelle unterbrochen fällt das gesamte Netz aus. In der Praxis versucht man dies durch mehrfache Verkabelung des Rings, oder dadurch, das man erlaubt Nachrichten in beide Richtungen zu senden, zu umgehen. |
Bäume
|
Technisch gesehen ist eine Baumverkabelung eine Sternverkabelung, der man eine Hierarchie unterlegt hat, um sie besser wartbar zu machen. Die inneren Knoten des Baumes bilden dabei Sterne Ein typisches Beispiel für eine baumartige Vernetzung ist die Organisation im Internet. Pakete laufen den Baum hinauf, bis zu einem Verteiler der den Zielrechner (oder wenigstens dessen Domain) kennt und von dort den Baum wieder hinunter zum Zielrechner. Auf die Einzelheiten kommen wir später noch. |
Sonstige
Natürlich lassen sich noch andere Möglichkeiten zur Vernetzung von Rechnern finden. Da gibt es noch das voll vermaschte Netz, bei dem von jedem Rechner zu jedem Rechner eine physikalische Verbindung existiert , Netze die durch Verbindung von Ringen an einzelnen Knotenrechnern entstehen, Bäume bei denen einzelne Knoten aus Ringen bestehen und jede mögliche Mischform aus den erwähnten Topologien.
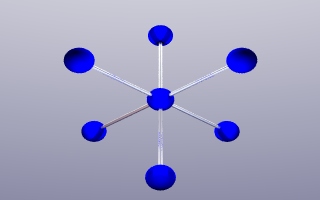 Die Sterntopologie entspricht der
klassischen Mainframe-Terminal-verbindung.
Die Sterntopologie entspricht der
klassischen Mainframe-Terminal-verbindung.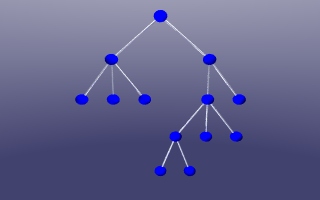 Es mag für
einen Laien zwar etwas ungewohnt sein, aber in der EDV wachsen
Bäume hierarchisch von oben (der Wurzel) nach unten (zu den
Blättern).
Es mag für
einen Laien zwar etwas ungewohnt sein, aber in der EDV wachsen
Bäume hierarchisch von oben (der Wurzel) nach unten (zu den
Blättern).